The speed of an object is given by:
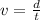
For the first part we know that the helicopter can travel 425 miles against a 935 headwind, the resultant speed of the helicopter will be its speed in still air minus the velocity of the wind, then we have:

For the scond part the resultant speed of the helicopter is the velocity of the wind plus the velocity of the helicopter, then we have:
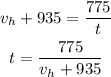
Since the time is equal we have that:

Therefore, the velocity of the helicopter is 3205.72 mph