Given:
The first method of payment follows a sequence:
1, 2, 4, 8,...
The second method of payment is a lump sum of $2 million
The final amount for the first method can be found using the formula:
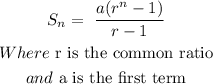
a = 1
r = 2
n =22
Substituting the values:
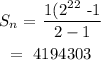
The final amount is $4194303
Hence, the first method would result in the greater payment because it would yield $4 million while the second method would yield $2 million