Question

For each value of x Determine whether it is a solution

Answer 1

Given the inequality

`1-8x\ge-39`

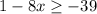
Let us evaluate for the value of x

Subtract 1 from both sides

`\begin{gathered} 1-8x-1\ge-39-1 \\ 1-1-8x\ge-40 \\ 0-8x\ge-40 \\ -8x\ge-40 \end{gathered}`

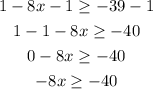
Divide both sides by -8

`(-8x)/(-8)\ge(-40)/(-8)`

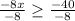
Note: The sign will change whenever you have the coefficient to be negative.

Therefore,

`x\leq5`

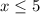
With the result above, let us now confirm whether the given values are solutions or not.

Hence,

`\begin{gathered} 10\text{ No, it is not a solution.} \\ -2\text{ Yes, it is a solution} \\ 5\text{ Yes, it is a solution} \\ -5\text{ Yes, it is a solution.} \end{gathered}`