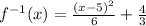Question

Can somebody help me with 10-13 ? I don’t know how to do the inverse of the functions

Answer 1

Problem N 10

we have the function

`f(x)=9+√(4x-4)`

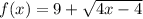
Find out the inverse

Let

y=f(x)

`y=9+4x-4`

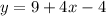
step 1

Exchange the variables (x for y and y for x)

`x=9+√(4y-4)`

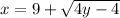
step 2

Isolate the variable y

`\begin{gathered} x=9+√(4y-4) \\ x-9=√(4y-4) \\ squared\text{ both sides} \\ (x-9)^2=4y-4 \\ 4y=(x-9)^2+4 \\ y=((x-9)^2)/(4)+(4)/(4) \\ \\ y=((x-9)^(2))/(4)+1 \end{gathered}`

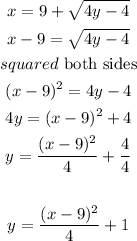
therefore

The inverse function is

`f^(-1)(x)=((x-9)^(2))/(4)+1`

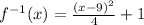
Problem N 11

we have the function

`f(x)=√(6x-8)+5`

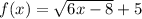
Find out the inverse

Let

y=f(x)

`y=√(6x-8)+5`

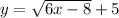
Exchange the variables

`\begin{gathered} x=√(6y-8)+5 \\ isolate\text{ the variable y} \\ x-5=√(6y-8) \\ squared\text{ on both sides} \\ (x-5)^2=6y-8 \end{gathered}`

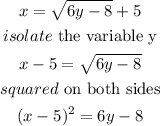
isolate the variable y

`\begin{gathered} 6y=(x-5)^2+8 \\ y=((x-5)^2)/(6)+(8)/(6) \\ \\ y=((x-5)^(2))/(6)+(4)/(3) \end{gathered}`

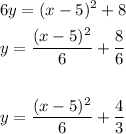
therefore

The inverse function is equal to

`f^(-1)(x)=((x-5)^(2))/(6)+(4)/(3)`