Question

2. Answer the following questions based on the two equations provided below.Here are two equations:Equation 1: 6x + 4y = 34Equation 2:5x - 2y = 152a. Decide whether each (x, y) pair is a solution to one equation, bothequations, or neither of the equations. *

Answer 1

To answer this question, we have to evaluate each equation at the x-entry of each point. If the result of the evaluation is equal to the y-entry of the point, then it is a solution.

1.- (3,4), evaluating the first equation at 2, we get:

`\begin{gathered} 6\cdot3+4y=34, \\ 18+4y=34. \end{gathered}`

Solving for y, we get:

`\begin{gathered} 4y=34-18, \\ y=(16)/(4)=4. \end{gathered}`

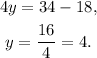
Therefore the point is a solution to the first equation. Also, point (3,2) is not a solution to the first equation.

Evaluating the second equation at x=3, we get:

`15-2y=15.`

Solving for y, we get:

`\begin{gathered} -2y=0, \\ y=0. \end{gathered}`

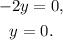
Therefore, points (3,4) and (3,2) are not solutions to the second equation.

Evaluating the first equation at x=4, we get:

`24+4y=34.`

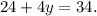
Solving for y, we get:

`\begin{gathered} 4y=34-24=10, \\ y=(10)/(4)=2.5. \end{gathered}`

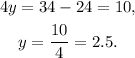
Therefore, point (4,2.5) is a solution to the first equation.

Evaluating the second equation at x=4, we get:

`20-2y=15.`

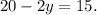
Solving for y, we get:

`\begin{gathered} 5=2y, \\ y=(5)/(2)=2.5. \end{gathered}`

Therefore, (4,2.5) is a solution to both equations.

Evaluating the first equation at x=5, we get:

`30+4y=34.`

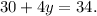
Solving for y, we get:

`\begin{gathered} 4y=4, \\ y=1. \end{gathered}`

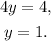
Therefore, point (5,5) is not a solution to the first equation.

Evaluating the second equation at x=5, we get:

`25-2y=15.`

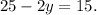
Solving for y, we get:

`\begin{gathered} 10=2y, \\ y=5. \end{gathered}`

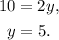
Therefore, (5,5) satisfies the second equation.

Answer:

(3,4) First equation.

(4,2.5) Both equations.

(5,5) Second equation.

(3,2) Neither.