Question

I need help with #15 (part a, b, and c)

Answer 1

Part A.

Let x be the number of months. Since the rate is $44 per month and the initial fee is $48, the linear model is:

`C(x)=44x+48`

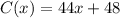
where C(x) denotes the total cost.

Part B.

In this case, we must substitute x=6 into our linear model. It yields,

`C(6)=44(6)+48`

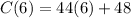
which gives

`\begin{gathered} C(6)=264+48 \\ C(6)=312 \end{gathered}`

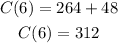
Therefore, after 6 months, the total cost will be $312.

Part C.

In this case, the second company has a rate of $62 per month with no initial fee. Then, the linear model for the second company is

`\begin{gathered} B(x)=62x+0 \\ or\text{ equivalently, } \\ B(x)=62x \end{gathered}`

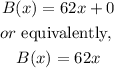
where now B(x) denotes the total cost for the second company.

Then, since you have $620, we can compare both companies by substituting the total cost of $620 into the two linear models, that is,

`\begin{gathered} 620=44x+48 \\ \text{and} \\ 620=62x \end{gathered}`

and finc x for each model.

Then, the first model yields,

`\begin{gathered} 44x=620-48 \\ 44x=572 \\ x=(572)/(44) \\ x=13\text{ months} \end{gathered}`

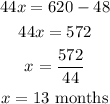
and the second equation gives

`\begin{gathered} x=(620)/(62) \\ x=10\text{ months} \end{gathered}`

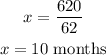
By comparing both result, we can see that the best choice in the first company with 13 months