Given:
The linearized regression line model;
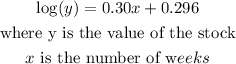
Given:
y = $200
Substituting the value of y in the model to get x,

Therefore, the best approximation of the number of weeks that will pass before the value of the stock reaches $200 is 6.7
Hence, the correct answer is option C.