To save for Malcom's education, his parents put $1,200 into a savings account when
Malcom was born in 2006. Every birthday, Malcolm's parents deposit 10% more than the
previous year.
Part A
In this problem we have an exponential function of the form
y=a(1+r)^x
where
a is the initial deposit
r is the rate of change
x is the number of years
y is the amount deposited in the saving account
so
we have
a=$1,200
r=10%=0.10
substitute
y=1,200(1+0.10)^x
y=1,200(1.10)^x --------> explicit formula
Part B
2006 -----> For x=0 -------> y=$1,200
2010 -----> For x=4 -----> y=$1,756.92
2014 ----> For x=8 -----> y=$2,572.31
2018 ----> For x=12 ----> y=$3,766.11
2022 ----> For x=16 ----> y=$5,513.97
Part C
we have an geometric sequence
To find out the sum
we use the formula

where
a is the first term
n is the number of terms
r is the common ratio
In this problem
a=$1,200
r=1.1
n=18
substitute
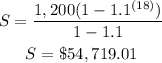
answer Part C is $54,719.01