Question

Giving a test to a group of students, the grades and gender are summarized below ABCTotalMale521118Female7181338Total12202456If one student is chosen at random,Find the probability that the student was male GIVEN they got a 'B'. Round your answer to at least 3 decimal places.

Answer 1

In conditional probability, we write this as P(B | A), or the conditional probability of B given that A has occured. It is given as

`P(B|A)=\frac{P(B\text{ and }A)}{P(A)}`

The probability that a male student AND has they got B is

`\begin{gathered} P(\text{Male and got B})=\frac{\text{Total number of male who got B}}{\text{Total number of students}} \\ P(\text{Male and got B})=(2)/(56) \end{gathered}`

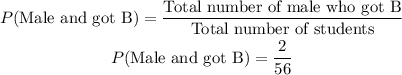
The probability that a student got B is

`P(\text{Student got B})=(20)/(56)`

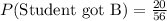
Putting it together we have

`\begin{gathered} P(\text{Male given they got B})=\frac{P(\text{Total number of male student who got B})}{P(\text{Student got B})} \\ P(\text{Male given they got B})=((2)/(56))/((20)/(56)) \\ P(\text{Male given they got B})=(2)/(20) \\ P(\text{Male given they got B})=0.1 \end{gathered}`

Therefore, the probability that the student was male GIVEN they got a 'B' is 0.1