Question

the world is using crude oil every year. in 2000 the world used about 76 million barrels a day and in 2010 the world used about 87 barrels a day. Assuming this is a linear trend come up with an equation for this. in addition if consumption is not curved how many will we use in 2050.

Answer 1

In order to create an equation for this case, let's use the slope-intercept form of the linear equation:

`y=mx+b`

Where m is the slope and b is the y-intercept.

In order to find the values of m and b, let's use two ordered pairs (x, y) that are solution to the equation.

Using the variable x to represent the number of years after 2000 and the variable y to represent the number of million barrels, we have the points (0, 76) and (10, 87), so:

`\begin{gathered} (0,76)\colon \\ 76=0m+b \\ b=76 \\ \\ (10,87)\colon \\ 87=10m+76 \\ 10m=87-76 \\ 10m=11 \\ m=(11)/(10) \end{gathered}`

So our equation is:

`y=(11)/(10)x+76`

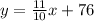
Now, in order to find the number of million barrels for 2050, we just need to calculate the value of y for x = 50, so we have:

`\begin{gathered} y=(11)/(10)\cdot50+76 \\ y=11\cdot5+76 \\ y=55+76 \\ y=131 \end{gathered}`

So the number of barrels that will be used in 2050 is 131 million barrels.