Question

The average height of a certain age group of people is 53".The standard deviation is 4".If the variable is normally distributed, find the probability that a randomly selected individual's height will be between 50 and 55:options are:a.)0.0668b.) 0.4649c.) 0.0228d.) 0.0934

Answer 1

Data

• The data is normally distributed.

,

• Average: 53

,

• Standard deviation: 4

,

• Random individual: between 50 and 55.

Procedure

As it is normally distributed, we have to use Z:

`Z=(x-\mu)/(\sigma)`

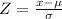
Replacing our values for 50 and 55:

• 50

`Z=(50-53)/(4)=-0.75`

• 55

`Z=(55-53)/(4)=0.5`

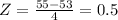
Therefore, our probability is equal in terms of Z:

`P(50To find the probability, we have to subtract as follows:[tex]P(-0.75-0.75)`

Using the Standard Normal Table we can see that:

`P(Z<0.50)=0.6915`

While the other value we need:

`P(Z>-0.75)=0.2266`

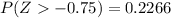
Finally:

[tex]P(-0.75Answer: b.