Question

Graph the function f. Then determine whether or not the function is continuous.

Answer 1

Given the function, to graph it and solve the problem, follow the steps below.

Step 01: Choose two points to graph the first piece of the function.

Let's choose x = -2 and x = -1. Althought x = -1 is not included in the first function, it is the limit. So, let's evaluate it.

First, let's substitute x by -2 and find y.

`\begin{gathered} f(x)=-x+3 \\ f(-2)=-(-2)+3 \\ f(-2)=+2+3 \\ f(-2)=5_{} \end{gathered}`

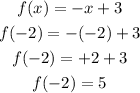
Now, let's find f(-1):

`\begin{gathered} f(x)=-x+3 \\ f(-1)=-(-1)+3 \\ f(-1)=1+3 \\ f(-1)=4 \end{gathered}`

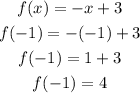
So, the function has a point (-2, 5) and ends at (-1, 4).

Step 03: Choose two points to graph the second piece of the function.

The second piece of the function is true for x ≥ -1.

Let's choose x = -1 and x = 0.

First, let's substitute x by -1:

`\begin{gathered} f(x)=-3x+1 \\ f(-1)=-3\cdot(-1)+1 \\ f(-1)=3+1_{} \\ f(-1)=4_{} \end{gathered}`

Second, let's substitute x by 0:

`\begin{gathered} f(0)=-3\cdot0+1 \\ f(0)=0+1 \\ f(0)=1 \end{gathered}`

So, the function has the points (-1, 4) and (0, 1).

Step 03: Plot the points in the graph and connect them to draw the graphs.

Plotting the points (-2, 5) and (-1, 4) (not included, open interval) for the first function (orange) and the points (-1, 4) and (0,1) for the second function (green):

The function is continuous since the limit when the function goes to -1 is 4.

As can be seen in the graph, the function does not present any discontinuity.

Answer: The function is continuous.