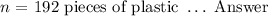Question

Mike had a piece of plastic that was 72feet long. He cut the plastic into 3/8-foot long pieces. How many pieces ofplastic did Mike cut?

Answer 1

Mike had a piece of plastic of a certain length. The length ( L ) is defined as:

`L\text{ = 72 feet}`

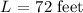
He deiced to cut the entire length ( L ) of the plastic into smaller pieces of equal length. The length of each piece ( l ) is defined as:

`l\text{ = }(3)/(8)\text{ foot}`

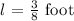
We will define the number of pieces he has after cutting the entire plastic as follows:

`n\text{ = Number of equally cut pieces of plastic}`

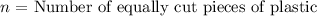
We will now set up an equation that relates ( n ) number of small pieces with length ( l ) that must equate to the entire length of the large plastic ( L ) as follows:

`n\cdot l\text{ = L}`

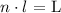
We can now plug in the respective quantities and solve for the ( n ) number of pieces that Mike cut as follows:

`\begin{gathered} n\text{ = }(L)/(l) \\ \\ n\text{ = }(72)/((3)/(8)) \end{gathered}`

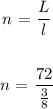
Now we will use the division to multiplication conversion rule by reciprocating the fraction ( 3 / 8 ) in the denominator and multiplying it with the numerator as follows:

`n\text{ = 72 }\cdot\text{ }(8)/(3)`

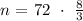
Simplify for the integer ( n ):

`n\text{ = 192 pieces of plastic }\ldots\text{ Answer}`