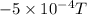Given
Current in the wires,
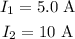
The distance between the wires,
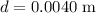
To find:
The magnetic field between the wires.
Step-by-step explanation:
Let O be the mid point between the wires.
The magnetic field due to the wire carrying the current
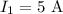
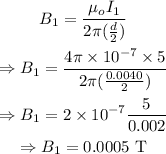
The magnetic field goes into the plane of the paper.
Again,
The magnetic field due to the wire carrying the current
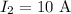
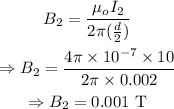
The magnetic fields goes out of the plane of the paper.
Thus the resultant magnetic field is:
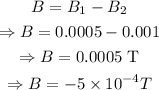
Conclusion
Thus the required answer is: