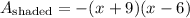Question

Write down an expression in factored form for the shaded area in the figure.

Answer 1

The given figure is a rectangle.

Recall that the area of a rectangle is given by

`A=L\cdot W`

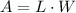
Where L is the length and W is the width of the rectangle.

The area of the shaded region can be obtained by subtracting the area of the inside region from the outside region.

The area of the outside region is

`A_{\text{outside}}=L\cdot W=9\cdot6=54`

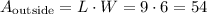
The area of the inside region is

`A_{\text{inside}}=L\cdot W=(x+3)_{}\cdot x=x^2+3x`

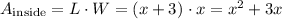
So, the area of the shaded region is

`\begin{gathered} A_{\text{shaded}}=A_{\text{outside}}-A_{\text{inside}} \\ A_{\text{shaded}}=54-(x^2+3x) \\ A_{\text{shaded}}=54-x^2-3x \\ A_{\text{shaded}}=-x^2-3x+54 \end{gathered}`

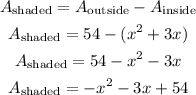
Finally, let us factor out the expression

`\begin{gathered} A_{\text{shaded}}=-x^2-3x+54 \\ A_{\text{shaded}}=-(x^2+3x-54) \\ A_{\text{shaded}}=-(x^2+9x-6x-54) \\ A_{\text{shaded}}=-((x^2+9x)(-6x-54)) \\ A_{\text{shaded}}=-(x(x^{}+9)-6(x+9)) \\ A_{\text{shaded}}=-(x^{}+9)(x-6) \end{gathered}`

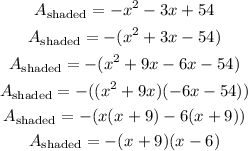
Therefore, the expression in factored form for the shaded area is

`A_{\text{shaded}}=-(x^{}+9)(x-6)`