Question

A man attaches a divider to an outdoor faucet so that water flows through a single pipe of radius 8.05 mm into 4 pipes, Each with a radius of 5 mm. If water flows through the single pipe at 1.95 m/s, calculate the speed in meters per second of the water in the narrower pipes.

Answer 1

We are asked to determine the velocity of flow in a pipe. To do that we must determine first the volumetric rate of fluid in the larger pipe. We use the following equation:

`Q=Av`

Where:

`\begin{gathered} Q=\text{ flow rate} \\ A=\text{ cross-sectional area} \\ v=\text{ velocity} \end{gathered}`

Now, we plug in the values for the larger pipe. We use the area of a circle:

`Q=(\pi r_1^2)v`

Now, we substitute the values:

`Q=\pi(0.00805m)^2(1.95(m)/(s))`

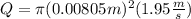
Solving the operations:

`Q=0.000396(m^3)/(s)`

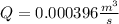
Since there are 4 pipes with the same radius this means that the flow in a single pipe is 1/4 of the flow of the larger pipe:

`Q_0=(0.000396(m^3)/(s))/(4)=0.0000992(m^3)/(s)`

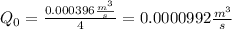
Now, to determine the velocity we use the same equation:

`Q_0=A_0v_0`

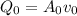
Now, we divide both sides by the area:

`(Q_0)/(A_0)=v_0`

Now, we plug in the values:

`\frac{0.0000992(m^3)/(s)}{\pi(0.005m){}^2}=v_0`

Solving the operations:

`1.26(m)/(s)=v_0`

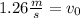
Therefore, the velocity in each individual pipe is 1.26 m/s.