Question

Heather can clean an attic in 16 hours . Perry can clean the same attic in 8 hours . Find how long it would take them if they worked together .

Answer 1

Step 1: Assume that there is the same work to be done.

Let t be the time it will take both of them to finish the work.

Then Heather can do

`\begin{gathered} \frac{t}{16\text{ }}\text{ job per hour} \\ \end{gathered}`

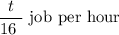
while Perry can do

`(t)/(8)\text{ job per hour}`

Step 2: Assume that both of them worked together, then we have that :

`\begin{gathered} (t)/(16)\text{ + }\frac{t}{8\text{ }}\text{ = }\frac{t\text{ + }2\text{ t }}{16}\text{ = }(3t)/(16) \\ \end{gathered}`

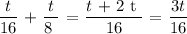
Step 3: We want to find the time it will take both of them to work together to finish the same job.

`\begin{gathered} \frac{3t}{16\text{ }}\text{ = 1} \\ \text{cross - multiply, we have that:} \\ 3t\text{ = 16} \\ \text{Divide both sides by 3, we have that :} \\ t\text{ =}(16)/(3)\text{ hours} \\ \text{t = 5}(1)/(3)\text{ hours} \end{gathered}`

CONCLUSION: It will take

`5\text{ }(1)/(3)\text{ hours for both of them to work together to finish the same job.}`