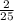We will investigate the fraction of non-fiction biography books in a library.
There are certain proportions that are given as follows:
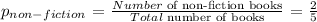
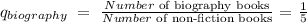
To determine the number of non-fictional biography books we will develop a compound proportions that would leave to following fraction:
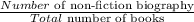
We can write the above fraction as a compounding off two given fraction ( p and q ) as follows:

Therefore, the fraction of non-fiction biography is: