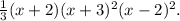Question

Use the given information about the polynomial Graph to write the equation Degree 5. Roots of multiplicity 2 at x=-3 and x=2 and a root of multiplicity 1 at x=-2. Y-intercept at (x,y) = (0,24)Y=_

Answer 1

We know that the polynomial has roots of multiplicity 2 at x=-3 and x=2, therefore, it must be of the form:

`Y(x)=P(x)(x+3)^2(x-2)^2.`

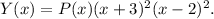
Now, we are given that the polynomial has a root at x=-2, we get that:

`P(x)=k(x+2)\text{.}`

Therefore:

`Y(x)=k(x+2)(x+3)^2(x-2)^2.`

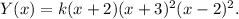
To determine the value of k we use the fact that the y-intercept is at (0,24):

`Y(0)=24=k(0+2)(0+3)^2(0-2)^2=k\cdot2\cdot9\cdot4=72k.`

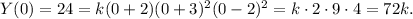
Solving the above equation for k, we get:

`k=(24)/(72)=(1)/(3)\text{.}`

Finally, substituting the value of k, we get that:

`Y(x)=(1)/(3)(x+2)(x+3)^2(x-2)^2.`

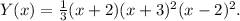
Answer:

`(1)/(3)(x+2)(x+3)^2(x-2)^2.`