Question

A kite’s diagonal is 3 times the length of the other diagonal. the kite has an area of 13.5 m squared. what is the length of each diagonal?

Answer 1

We have a kite with one diagonal length being 3 times the length of the other diagonal.

We also know that the area is 13.5 m².

A kite has two perpendicular diagonales, so its area can be calculated as half the product of the lengths of the diagonals.

Then, if we have the short diagonal with length d, the long diagonal will have a length 3d.

The area then can be expressed as:

`\begin{gathered} A=(1)/(2)(d_1*d_2) \\ A=(1)/(2)(d*3d) \\ A=(3)/(2)d^2 \end{gathered}`

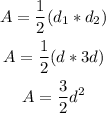
As the area is 13.5 m², we can calculate d as:

`\begin{gathered} A=13.5 \\ (3)/(2)d^2=13.5 \\ d^2=(2)/(3)*13.5 \\ d^2=9 \\ d=√(9) \\ d=3 \end{gathered}`

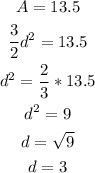
We have the length of the short diagonal d = 3 m.

Then, the long diagonal will have a length 3*3 = 9 m.

Answer: the diagonals are 3 m and 9 m long.