Notice that the triangle ABC is an isosceles triangle, since the sides AB and CB have the same measure. Since congruent sides of an isosceles triangle are opposite to congruent angles, then:

Now, observe the triangles BAD and BCE. We know that:
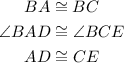
(Note: The angle BAD is the same as BAC, as well as the angle BCE is the same as BCA).
Then, from the SAS congruence criterion, the triangles BAD and BCE are congruent:

On the triangles BAD and BCE, the angles BDA and BEC are corresponding angles, since they are opposite to congruent sides.
On the other hand, since Corresponding Parts of Congruent Triangles are Congruent, then:
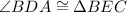
Finally, since the angle BDA is the same as BDE and the angle BEC is the same as BED, then:
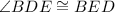
Which completes the proof.