Solution:
Given that orange costs 1.29 per pound, this implies that
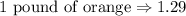
Given that Julie bought 5 pounds of oranges, let y represent the cost of her purchase.
This implies that
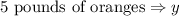
Thus, the total cost of her purchase is evaluated as
![\begin{gathered} 1\text{ pound of orange}\operatorname{\Rightarrow}1.29 \\ 5\text{ pounds of oranges}\operatorname{\Rightarrow}y \\ cross-multiply, \\ y*1\text{ pound of orange=1.29}*5\text{ pounds of oranges} \\ divide\text{ both sides by 1 pound of orange,} \\ \frac{y*1\text{ }pound\text{ }of\text{ }orange}{1\text{ pound of orange}}\text{=}\frac{1.29*5\text{ }pounds\text{ }of\text{ }oranges}{1\text{ pound of orange}} \\ y=1.29*\frac{5\text{ }pounds\text{ }of\text{ }oranges}{1\text{ pound of orange}} \\ \Rightarrow y=6.45 \end{gathered}]()
Hence, Julie's total cost of her purchase is 6.45