Question

Hello, I need some assistance with this precalculus question, please?HW Q13

Answer 1

Okay, here we have this:

Considering the provided system of equation we are going to solve it, using row operation, so we obtain the following:

Then we have the following matrix of coefficients:

`\begin{bmatrix}-{1} & {1} & {1} & -{3} \\ {-1} & {5} & {-15} & {-27} \\ {6} & -{3} & -{18} & {0} \\ {} & {\placeholder{⬚}} & {\placeholder{⬚}} & {\placeholder{⬚}}\end{bmatrix}`

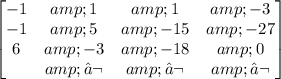
Interchanging row 1 and 3:

`\begin{bmatrix}{6} & -{3} & {-18} & {0} \\ {-1} & {5} & -{15} & {-27} \\ {-1} & {1} & {1} & {-3} \\ {\placeholder{⬚}} & {\placeholder{⬚}} & {\placeholder{⬚}} & {\placeholder{⬚}}\end{bmatrix}`

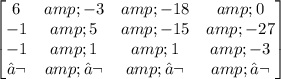
Doing the operation Row 2=Row 2+1/6 Row 1:

`\begin{bmatrix}{6} & -{3} & {-18} & {0} \\ 0 & {(9)/(2)} & {-18} & {-27} \\ {-1} & {1} & {1} & {-3} \\ {\placeholder{⬚}} & {\placeholder{⬚}} & {\placeholder{⬚}} & {\placeholder{⬚}}\end{bmatrix}`

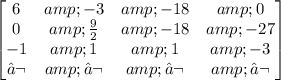
Doing the operation Row 3=Row 3+1/6 Row 1:

`\begin{bmatrix}{6} & -{3} & -{18} & {0} \\ {0} & {(9)/(2)} & {-18} & -{27} \\ {0} & {(1)/(2)} & -2 & -3 \\ {\placeholder{⬚}} & {\placeholder{⬚}} & {\placeholder{⬚}} & {\placeholder{⬚}}\end{bmatrix}`

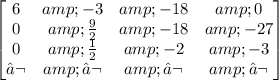
Doing the operation Row 3=Row 3-1/9 Row 2:

`\begin{bmatrix}{6} & {-3} & {-18} & {0} \\ {0} & {(9)/(2)} & {-18} & {-27} \\ {0} & {0} & {0} & {0} \\ {\placeholder{⬚}} & {\placeholder{⬚}} & {\placeholder{⬚}} & {\placeholder{⬚}}\end{bmatrix}`

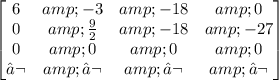
Doing the operation Row 2=(2/9)Row 2:

`\begin{bmatrix}{6} & -{3} & {-18} & {0} \\ {0} & {1} & {-4} & {-6} \\ {0} & {0} & {0} & {0} \\ {\placeholder{⬚}} & {\placeholder{⬚}} & {\placeholder{⬚}} & {\placeholder{⬚}}\end{bmatrix}`

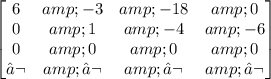
Doing the operation Row 1=(1/6)Row 6:

`\begin{bmatrix}{1} & {0} & -{5} & {-3} \\ {0} & {1} & {-4} & {-6} \\ {0} & {0} & {0} & {0} \\ {\placeholder{⬚}} & {\placeholder{⬚}} & {\placeholder{⬚}} & {\placeholder{⬚}}\end{bmatrix}`

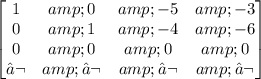
From there we get the following two equations:

x-5z=-3 -> x=-3+5z

y-4z=-6 -> y=-6+4z

Finally we obtain that there are infinitely many solutions. The solutions can be written as (x, y, x) . Then the correct answer is the option B.