Question

I need help on understanding on how to make this equation equal to zero?

Answer 1

`f(x)=7x^4-17x^2-12`

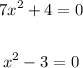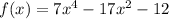
Factor f(x):

1- Rewrite -17x² as a difference:

`=7x^4+4x^2-21x^2-12`

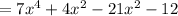
2- Factor x² as a common factor of the first two terms:

`=x^2(7x^2+4)-21x^2-12`

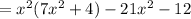
3- Factor -3 as common factor in the last two terms:

`=x^2(7x^2+4)-3(7x^2+4)`

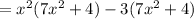
4-Factor (7x²+4):

`f(x)=(7x^2+4)(x^2-3)`

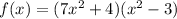
Make the equation equal to x:

`(7x^2+4)(x^2-3)=0`

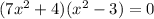
If the product of two numbers is zero, then at least one of the factors is 0:

`\begin{gathered} 7x^2+4=0 \\ \\ x^2-3=0 \end{gathered}`