If "a" is a positive number, then we can perform the following transformations:
1) A shift to the left (or to the right)
2) A shift up (or down)
1)
This transformation can be expressed as:
![\begin{gathered} f\mleft(x\mright)\rightarrow f\mleft(x+a\mright)\text{ \lparen Shift a units to the left\rparen} \\ f\mleft(x\mright)\operatorname{\rightarrow}f\mleft(x-a\mright)\operatorname{\lparen}\text{Shift a units to the right}\operatorname{\rparen} \end{gathered}]()
2)
This transformation can be expressed as:
![\begin{gathered} f\mleft(x\mright)\rightarrow f\lparen x)+a\text{ \lparen Shift a units up\rparen} \\ f\mleft(x\mright)\operatorname{\rightarrow}f\lparen x)-a\operatorname{\lparen}\text{Shift a units down}\operatorname{\rparen} \end{gathered}]()
From this, if we have:
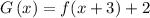
Then, we have:
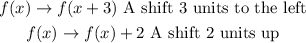
If we combine both transformations, we have a final graph of G(x) that is shifted 3 units to the left and 2 units up with respect to the graph of f(x)