Question

I need help with this problem I'll send the question picture

Answer 1

`PC\text{ = 2(3x-3) = 36}`

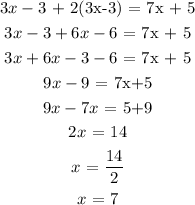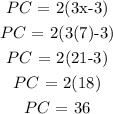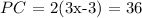
Here, we want to find the length of PC

As we can see from the figure provided, the point P represents the centroid of the triangle

The centroid divides each median length into lengths of ratio 2 to 1

SC is divided into 2 parts; SP and PC; with the length of PC twice that of SP

The addition of the two will give SC

Thus, we have it that;

`\begin{gathered} 3x-3\text{ + 2(3x-3) = 7x + 5} \\ 3x-3+6x-6\text{ = 7x + 5} \\ 3x+6x-3-6\text{ = 7x + 5} \\ 9x-9\text{ = 7x+5} \\ 9x-7x\text{ = 5+9} \\ 2x\text{ = 14} \\ x\text{ = }(14)/(2) \\ x\text{ = 7} \end{gathered}`
`\begin{gathered} PC\text{ = 2(3x-3)} \\ PC\text{ = 2(3(7)-3)} \\ PC\text{ = 2(21-3)} \\ PC\text{ = 2(18)} \\ PC\text{ = 36} \end{gathered}`