Question

Need help asappppppp

Answer 1

a.

Consider that the volume (V) of a cone with radius 'R' and height 'H' is given by,

`V=(1)/(3)\pi R^2H`

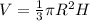
Substitute the values,

`\begin{gathered} V=(1)/(3)\pi(4)^2(3) \\ V=16\pi \end{gathered}`

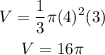
Therefore, option b is the correct choice.

b.

Consider that the volume (V') of a cylinder with radius 'R' and height 'H' is given by,

`V^(\prime)=\pi R^2H`

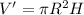
Solve for the ratio of volume of cone to that of cylinder as,

`(V)/(V^(\prime))=(((1)/(3)\pi R^2H))/((\pi R^2H))=(1)/(3)`

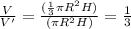
Therefore, option c is the correct choice.