Question

I think I did the first two right but need help with the length of the curve.

Answer 1

We have the following function, f(x)

`\sqrt{1+\left((1)/(√(1-x^2))\right)^2}`

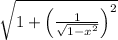
and, we need to find the riemann sum with n=3

`\int _{-(1)/(4)}^{(1)/(4)}\sqrt{1+\left((1)/(√(1-x^2))\right)^2}dx`

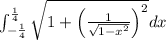
Let's use the following to find the right riemann sum

`\int_a^bf\left(x\right)dx\:\approx\sum_{n\mathop{=}1}^3f(x_i)*\Delta x`

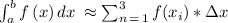
1st, let's calculate dx

`\Delta x=(b-a)/(n)=(0.25+0.25)/(3)=(1)/(6)`

2nd, calculate each f(xi)

`\begin{gathered} x_1=-(1)/(4)+(1)/(6)=-(1)/(12),f(x_1)=\sqrt{(287)/(143)} \\ x_2=-(1)/(12)+(1)/(6)=(1)/(12),f(x_2)=\sqrt{(287)/(143)} \\ x_3=(1)/(12)+(1)/(6)=(1)/(4),f(x_3)=\sqrt{(31)/(15)} \end{gathered}`

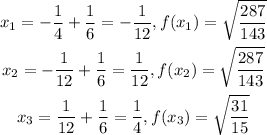
Now, let calculate the right riemann sum

`\sum_{n\mathop{=}1}^3f(x_i)*\Delta x=(1)/(6)*\left(\sqrt{(287)/(143)}+\sqrt{(287)/(143)}+\sqrt{(31)/(15)}\right)`

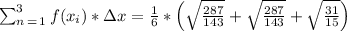
Solving, we get

`=0.7118`

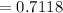
Thus, the answer is 0.7118