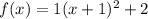Question

Find the equation of the quadratic function, f(x), in vertex form, whose graph is shown.f(x)=

Answer 1

Given the question in the image, the following are the solution steps to answer the question.

STEP 1: Write the standard vertex form for a quadratic equation.

`\begin{gathered} y=a(x-h)^2+k \\ where\text{ }(h,k)\text{ is the vertex} \end{gathered}`

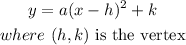
STEP 2: Get the vertex of the quadratic equation plotted

`Vertex=(h,k)=(-1,2)`

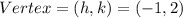
STEP 3: Get the value of a

To get the value of a, we pick a random point on the graph. We pick:

`(x,y)=(0,3)`

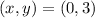
Substitute the known values into the form in Step 1 to get the value of a as seen below:

`\begin{gathered} 3=a(0-(-1))^2+2 \\ 3=a(1^2)+2 \\ 3=a+2 \\ 3-2=a \\ a=1 \end{gathered}`

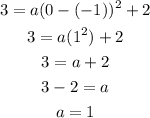
STEP 4: Get the vertex form of the equation

`\begin{gathered} a=1 \\ (h,k)=(-1,2) \\ \\ By\text{ substitution,} \\ y=1(x-(-1))^2+2 \\ y=1(x+1)^2+2 \end{gathered}`

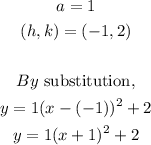
Hence, the vertex form of the equation is given as:

`f(x)=1(x+1)^2+2`