The reference angle of 117° is
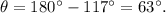
Therefore, we have to determine an angle in each quadrant with a reference angle of 63°. To illustrate the solution, we will use the following diagram as a reference:
From the above diagram, we get that:
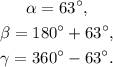
Simplifying the above results, we get:
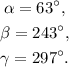
Finally, we get that, in the first quadrant the angle that has the same reference angle as 117° is:
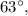
in the second quadrant is:
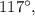
in the third quadrant is:
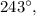
and in the fourth quadrant is:
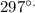
Answer:
