Given data:
Position of the particle along the x-axis;
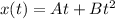
Here, A and B are constants with A=-3.15 m/s and B=2.4 m/s².
Therefore,
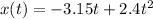
The velocity of the particle is given as,
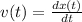
Substituting x(t),
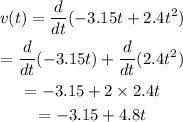
The time when the velocity will be zero is calculated by substituting v(t)=0 in the above expresion,
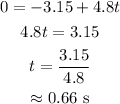
Therefore, the position of the particle when the velocity is zero is calculated by substituting t=0.66 s in the equation for the position of the particle,
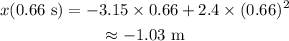
Therefore, the position of the particle when the velocity is zero is -1.03 m (1.03 m to the left of its initial position).