Question

choose a value for x and then solve to find the corresponding y value that makes that equation true . a) 6x = 7y b) 5x + 3y = 9 c) y + 5 - 1/3 x = 7

Answer 1

For every equation, we have to choose a value for x, and solve for y.

For part a) we have that the equation is:

`6x=7y`

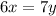
If we choose the following value for x:

`x=1`

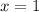
And substitute it in the equation, we find the value of y:

`\begin{gathered} 6(1)=7y \\ 6=7y \\ \text{Dividing both sides by 7:} \\ (6)/(7)=y \end{gathered}`

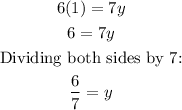
Answer for part a) when x=1, the value of y is y=6/7

For part b) we have the equation:

`5x+3y=9`

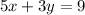
If we choose the following value for x:

`x=3`

and substitute it in the equation to find y:

`5(3)+3y=9`

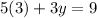
To solve for y, first, we solve the multiplication between 5 and 3:

`15+3y=9`

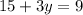
Now we subtract 15 to both sides:

`\begin{gathered} 3y=9-15 \\ 3y=-6 \end{gathered}`

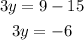
Finally, divide both sides by 3:

`\begin{gathered} (3y)/(3)=(-6)/(3) \\ y=-2 \end{gathered}`

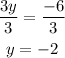
Answer for part b) when x=3, the value of y is y=-2

For part c) we have the equation:

`y+5-(1)/(3)x=7`

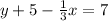
In this case, we can choose a value for x in such a way that we eliminate the fraction. For this, we can again choose the value:

`x=3`

And we substitute it:

`y+5-(1)/(3)(3)=7`

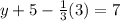
1/3 by 3 is equal to 1:

`y+5-1=7`

Next, combine the like terms on the left side 5-1 which is 4:

`y+4=7`

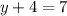
And finally, subtract 4 to both sides:

`\begin{gathered} y=7-4 \\ y=3 \end{gathered}`

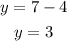
Answer for part c) when x=3, the value of y is y=3