Question

A certain company recorded the number of employee absences each week over a period of 10 weeks. The result is the data list 3, 5, 1, 2, 2, 4, 7, 4, 5, 5. Find the mean and standard deviation of the number of absences per week. Round the standard deviation to two decimal places. mean ___ daysstandard deviation ____ days

Answer 1

mean = 3.8 days

standard deviation = 1.72 days

Step-by-step explanation:

The mean can be calculated as the sum of all values divided by the number of values, so:

`\text{mean}=(3+5+1+2+2+4+7+4+5+5)/(10)=3.8`

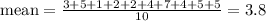
Therefore, the mean is 3.8 days.

Then, to know the standard deviation, we need to fill the following table:

data (data - mean)²

3 (3 - 3.8)² = 0.64

5 (5 - 3.8)² = 1.44

1 (1 - 3.8)² = 7.84

2 (2 - 3.8)² = 3.24

2 (2 - 3.8)² = 3.24

4 (4 - 3.8)² = 0.04

7 (7 - 3.8)² = 10.24

4 (4 - 3.8)² = 0.04

5 (5 - 3.8)² = 1.44

5 (5 - 3.8)² = 1.44

Then, the standard deviation is equal to:

`\begin{gathered} s=\sqrt[]{(0.64+1.44+7.84+3.24+3.24+0.04+10.24+0.04+1.44+1.44)/(10)} \\ s=\sqrt[]{(29.6)/(10)}=\sqrt[]{2.96}=1.72 \end{gathered}`

Therefore, the standard deviation is 1.72 seconds.