Step 1 - Write out the formula for the n-th term of a geometric sequence/progression.

from the sequence question, a is 1/27
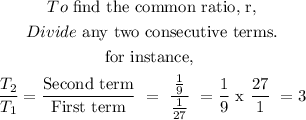
Therefore the common ratio is r is 3 and the first term a is 1/27
We need both the first term and the common ratio to get the term that gives us a value of 6,561.
Step2 - substitute the values for the first term and common ratio into the n-th term formula earlier written.
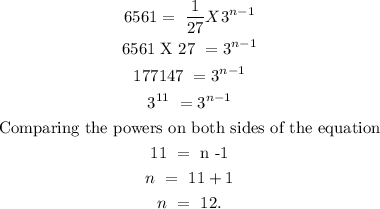
The term that gives 6561 in the sequence is 12