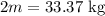Question

Two objects are placed so their centers are 1.65 meters apart, and the force between them is 8.09 x 10-10 newtons. What is the mass of each object if one has twice the mass of the other? Include units in your answers. Answer must be in 3 significant digits.

Answer 1

Given that the distance between two objects is r = 1.65 m

The force between the objects is

`F=8.09*10^(-10)\text{ N}`

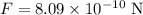
If the mass of object 1 is m then the mass of object 2 will be 2m

The gravitational force will be

`F=(Gm*2m)/(r^2)`

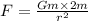
Here, G is the universal gravitational constant whose value is

`G=6.6*10^(-11)Nm^2kg^(-2)`

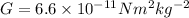
The mass can be calculated as

`m^{}=\sqrt{(Fr^2)/(2G)}`

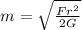
Substituting the values, the mass will be

`m=16.685\text{ kg}`

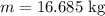
The mass of object 2 will be

`2m=33.37\text{ kg}`