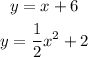Question

Use the graph of the systems of equations below to answer questions 1-210&4N76.3-4-3-2-10oB1. Choose yes or no to indicate which of the ordered pairs given is a point of intersection and solution tosystem above. (1 point)Ordered PairYes(-2,4)D(3,2)(-5,-4)(4, 10)O DOロロロロる2 O O O O

Answer 1

To get the solution to the system, we just need to look for the points in which the graphs intersect each other.

We can see that it occurs in two points:

These points are (-2, 4) and (4, 10).

To find the system of equations we have, we have to find the equations for each graph.

The blue one is a line, so we can find the equations using the two points we have:

`m=(y_2-y_1)/(x_2-x_1)=(10-4)/(4+2)=(6)/(6)=1`

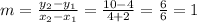
And:

`\begin{gathered} y-y_1=m(x-x_1)_{} \\ y-4=1(x+2) \\ y=x+2+4 \\ y=x+6 \end{gathered}`

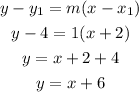
Now, we can already see that we only have one alternative with this equation.

We can just check wether the other equation is also correct. To do that, we can check wether the points of solutions are in the other graph.

The equation on the alternative is:

`y=(1)/(2)x^2+2`

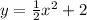
Checking for (-2, 4), we have:

`\begin{gathered} y=(1)/(2)(-2)^2+2 \\ y=(1)/(2)4+2 \\ y=2+2 \\ y=4 \end{gathered}`

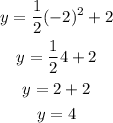
It checks out.

For (4, 10):

`\begin{gathered} y=(1)/(2)4^2+2 \\ y=(1)/(2)16+2 \\ y=8+2 \\ y=10 \end{gathered}`

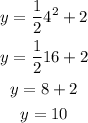
I also checks out.

So, the correct alternative for second part is:

`\begin{gathered} y=x+6 \\ y=(1)/(2)x^2+2 \end{gathered}`