Problem: find the sum of the first seven terms of the following sequence round to the nearest hundredth if necessary
6,-10,50/3
Solution: We have that the terms of the sequence are part of a geometric sequence. So, If a sequence is geometric there are ways to find the sum of the first n terms, denoted Sn, without actually adding all of the terms. To find the sum of the first Sn terms of a geometric sequence uses the formula 1:
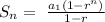
with r not equal to 1, and where n is the number of terms, a_1 is the first term and r is the common ratio. The common ratio is the ratio between a term and the term preceding it. Then in our case, a_1 = 6 and the common ratio is:
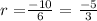
so, replacing the common radius and the first term in formula 1, (for n = 7) we have:
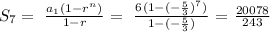
then, we can conclude that the sum of the first seven terms :
