Question

Find the area of the composite figure 5 km 4 km 3 km

Answer 1

The figure consists of a semi-circle and a triangle.

Hence,

`\text{ the area of the figure = area of the triangle }+\text{ area of the semi-circle}`

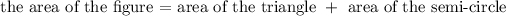
Given a triangle with base b and perpendicular height, h, then the area, A, of the triangle is given by

`A=(bh)/(2)`

In this case,

b = 3km, and h = 4km

therefore,

Given a semi-circle with diameter, d, the area, say S, of the semi-circle, is given by

`S=(\pi d^2)/(8)`
`\begin{gathered} \text{taking,} \\ \pi\approx3.142 \end{gathered}`

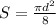
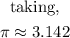
We must have that,

`S=(3.142d^2)/(8)`

In our case,

d = 4km

therefore,