Question

Alan deposited $4000 into an account with 2.8% interest compounded semiannually. Assuming that no withdrawals are made how much will he have in the account after 5 years? Round your answer to the nearest cent

Answer 1

$4596.63

Explanation:

Given:

• The Principal Alan deposited, P = $4000

,

• Annual Interest Rate, r = 2.8% = 0.028

,

• Compounding Period, k = 2 (Twice in a year)

,

• Time, t = 5 years

We want to determine how much he will have in the account after 5 years.

In order to carry out this calculation, use the compound interest formula below:

`A(t)=P(1+(r)/(k))^(tk)`

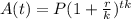
Substitute the values defined above:

`A(t)=4000(1+(0.028)/(2))^(2*5)`

Finally, simplify and round to the nearest cent.

`\begin{gathered} A(t)=4000(1+0.014)^(10) \\ =4000(1.014)^(10) \\ =\$4596.63 \end{gathered}`

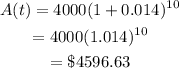
Alan will have $4596.63 in his account after 5 years.