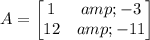Question

Match each value to the correct entry in matrix A.

Answer 1

`A=\begin{bmatrix}{1} & {-3} \\ {12} & {-11}\end{bmatrix}`

Step-by-step explanation

To find the elements of matrix A, we have to write the product AB first, using the letters a, b, c, and d. Remember that to multiply two matrices, we have to do the dot product of the rows of the first matrix and the columns of the second matrix. In this case, we have,

So, since we know what the matrix resulting from the product, we have four equations,

`\begin{gathered} \begin{cases}-a+3b=-10 \\ 2a-5b=17\end{cases} \\ \\ \begin{cases}-c+3d=-45 \\ 2c-5d=79\end{cases} \end{gathered}`

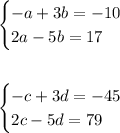
Note that the equations are in pairs, for (a, b) and for (c, d), so we have two systems of two equations to solve.

Solve both using the elimination method. Multiply the first equation by 2 and add the two equations in each system,

Now, knowing the values of b and d, we can find the values of a and c. Solve the first equation of each system for a and b respectively,

`\begin{gathered} a=10+3b \\ c=45+3d \end{gathered}`

Substitute the values of b and d and solve,

`\begin{gathered} a=10+3\cdot(-3)=10-9=1 \\ c=45+3(-11)=45-33=12 \end{gathered}`

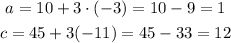
Hence, a = 1, b = -3, c = 12, and d = -11, and the matrix is,

`A=\begin{bmatrix}{1} & {-3} \\ {12} & {-11}\end{bmatrix}`