Question

If pp and qq vary inversely and pp is 30 when qq is 25, determine qq when pp is equal to 50.

Answer 1

The Solution:

Given that p and q are inversely related, we have that:

`p\propto(1)/(q)`

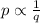
This means that:

`\begin{gathered} p=(1)/(q)* k \\ \\ p=(k)/(q) \\ \\ \text{ Where k=constant of variation.} \end{gathered}`

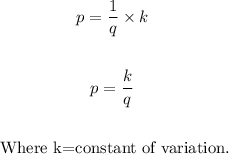
Given the initial condition (or values) that p =30 when q = 25.

Substituting these values in the relation above, we get

`30=(k)/(25)`

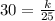
Cross multiplying, we get

`k=30*25=750`

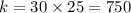
So, the formula connecting p and q is obtained as

`p=(750)/(q)`

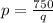
We are asked to find the value of q when p = 50.

Substitute 50 for p in the formula connecting p and q.

`50=(750)/(q)`

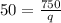
Cross multiplying, we get

`50q=750`

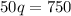
Dividing both sides by 50, we get

`\begin{gathered} (50q)/(50)=(750)/(50) \\ \\ q=15 \end{gathered}`

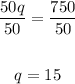
Therefore,