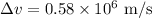Given data:
* The uncertainty in the measure of the location is given as,
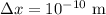
Solution:
According to the uncertainty principle, the theoretical limit to measure the momentum is,

where h is the Planck's constant,
Substituting the known values,
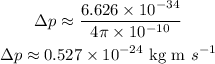
Thus, in advanced mathematics, the value of the momentum in kilogram meter per second is,
![\text{0}.527*10^(-24)\operatorname{kg}ms^(-1)]()
(B). The mass of the electron is,

Thus, the uncertainty in the electron speed is,
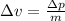
Substituting the known values,
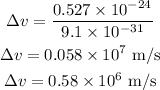
Thus, the uncertainty in the electron speed is,