Given:
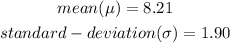
To Determine: The probability that a randomly selected individual will take less than 5 minutes to select a shoe purchase
Solution
P(x<5)
The z score formula is given as

Substitute the given into the formula
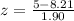
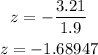
The probabilty would be

Hence, the probability is 0.045, which is unusual as it is less than 5%