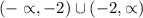First, we have a translation of 5 units right. That means the value of x is decreased by 5 units (x' = x - 5)
So we have:
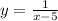
Then, we have a reflection over the x-axis, which means the value of the function changes signal (y' = -y)
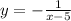
Finally, we have a translation of 2 units down, which means the value of the function is decreased by 2 units (y' = y - 2)
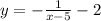
Adding a horizontal compression by a factor of 2 means the value of x will be multiplied by 2 (x' = 2x)
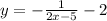
Graphing this function, we have:
The domain is all values x can assume. Since we have a fraction, its denominator can't be zero, so:
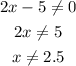
So the domain is:
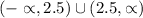
The range is all values y can assume. Since the fraction can't have a value of zero, we have:
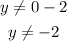
So the range is: