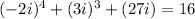If we have:
Then, the first option must be matched with -20. That is:
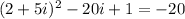
In this question, we need to be careful with the value of i^2 = -1, and we also need to expand the quadratics in every given expression.
2. For the next expression, we have:
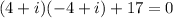
3. For the next expression, we have:
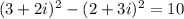
4. The result for the next expression is:
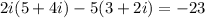
5. The result for the next expression is: