Question

Derive the equation of the parabola with a focus at (0, −4) and a directrix of y = 4. (2 points)

Answer 1

Answer: f(x)=-1/16 x^2

Answer 2

Equation of a parabola is given by

`\begin{gathered} (x-h)^2=4p(y-k) \\ where\text{ the focus is \lparen h, k + p\rparen} \\ directrix\text{ is y = k - p } \end{gathered}`

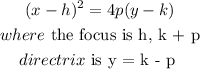
From the question, we have been given

`focus\text{ at \lparen0, -4\rparen and a directrix of y = 4}`

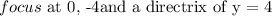
This means that the vertex is halfway at (0, 0) and the focal length p = 4

The equation becomes

`\begin{gathered} (x-h)^2=4p(y-k) \\ (x-h)^2=4py-4k \\ (x-h)^2+4k=4py \\ (x-h)^2*(1)/(4)+k=py \end{gathered}`

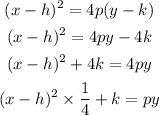
Now, note that k and h = 0, so we have

`\begin{gathered} (1)/(4)(x-0)^2+0=py \\ (1)/(4)(x^2)=py \\ y=(1)/(4p)(x^2) \end{gathered}`

So because this graph will be an "n" shape, so the focus will be negative, hence, we have

`\begin{gathered} y=-(1)/(4p)(x^2) \\ y=-(1)/(4*4)x^2 \\ y=-(1)/(16)x^2 \\ Hence\text{ } \\ f(x)=-(1)/(16)x^2 \end{gathered}`

Hence the answer is the third option