The Solution:
Given the properties:
Circle A:
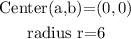
By the formula for the equation of a circle,

But

Substituting, we get
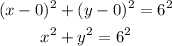
For Circle B:
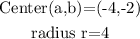
Substituting these values in the formula for the equation of a circle.
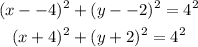
Graphing the two circles using the Desmos graph plotter, we have
Part B:
The transformation is a dilation by a scale factor of 4/6 (a shrink of circle A) and was shifted by 4 units left and 2 units down.
Part C:
The mapping shows that circle B is a shrink of circle A.
Circle A has its center at the origin (0,0) while the center of circle B is at (-4,-2)