Let x be the time Julia traveled on her way to the caves ( in hours), then
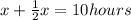
solving for x we get:
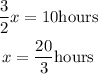
Now, we use the formula of the average speed for the speed on the way to the caves:
![AS=(360)/((20)/(3))\frac{\operatorname{km}}{h}]()
Therefore, the average speed on her way to the caves was 54 km/h.
Doing the same ( but the time being 1/2 x) for the average speed on her way back home we get 108 km/h.