Question

Leila is borrowing $65000 for 4 years. She is deciding between a loan at 6.95% per annum, compounded monthly, and a loan at 7% per annum, compounded annually.

Answer 1

The required formula to calculate the interest is given by is given by:

`\begin{gathered} I=P(1+(r)/(n))^(nt)-P \\ P\text{ = Initial Principal Balance} \\ r=\text{ interest rate} \\ n=\text{ number of times interest applied per time year} \\ t=\text{ the number of years} \end{gathered}`

Convert 6.95% to decimal:

`0.0695`

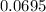
Substitute n=12, t=4, P = 65000, and r = 0.0695 into the equation:

`\begin{gathered} I=65000(1+(0.0695)/(12))^(12*4)-65000 \\ I\approx20762.80 \end{gathered}`

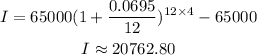
Therefore, the interest paid on the first option is approximately $20762.80

Using a similar procedure, it is found that the interest paid on the second option is approximately $20201.74

Therefore, the better deal is the second option and the interest paid is $20201.74