Question

What are the solutions for 0 is less than or equal to x or less than or equal to 360 degrees

Answer 1

Solve the trigonometric equation

`\cos ((x)/(2))-\sin (x)=0`

To express both trigonometric functions in terms of the same argument, we have to use some identities.

Please note the cos is of x/2 and the sine is of x

We'll use the identity known as the sine of the double angle:

sin(2A)=2sin(A)cos(A)

in this case, A=x/2, and the identity is now:

sin(x)=2sin(x/2)cos(x/2)

note we have now all the trigonometric functions with the same argument x/2

Substituting the new-found relationship in the original equation, we have

`\cos ((x)/(2))-2\sin ((x)/(2))\cos ((x)/(2))=0`

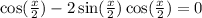
Now, we factor the expression by cos(x/2):

`\cos ((x)/(2))(1-2\sin ((x)/(2)))=0`

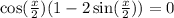
We have now a factored equation, both factors can be zero, which gives us two possible solutions:

`\cos ((x)/(2))=0,or1-2\sin ((x)/(2))=0`

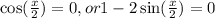
The first solution comes from cos(x/2)=0

There are several angles whose cosine is 0. They are 90°, 270°, 450°, and many more, thus:

x/2=90°

Solving

x=180°

This is our first solution since the angle lies in the interval (0,360°)

Now for the second solution:

`1-2\sin ((x)/(2))=0`

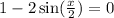
Solving for sin(x/2):

`\sin ((x)/(2))=(1)/(2)`

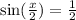
There are many angles whose sine is 1/2, like 30°, 150°, and others. Taking the first angle:

x/2=30° or x=60° is our second solution. One more remains

x/2=150° or x=300°

Summarizing, the whole set of solutions is

60°, 180°, 300°

The third choice is correct